Collision detection can be a very difficult subject for games programmers to get into because it is so poorly documented. One of the problems is that it is difficult to write down an algorithm that is suitable for all the possible applications. Collision detection algorithms can be a large drain on system resources and it is important to get the right balance between functionality and performance. Whilst they are important to the mechanics of the game, they do not add to the enjoyment of the game like a new graphical effect will. However, it is very important to get it right because the negative effects of say dropping through a floor for no apparent reason are serious.

This section will give a few example techniques that can be used. It is just a list of techniques I have used or thought about in the past and so it is not intended to be particularly comprehensive.

If you have a 2D space and are willing to accept some constraints a look-up table can be an efficient way to perform collision detection. Build an array that describes the 2D area to sufficient resolution and fill it with all the possible 'hits' in the scene. Collision detection is then simply a case of working out the position(s) where hits need to be checked and then checking the corresponding location(s) in the look-up table. (In the old days we used to use the graphics buffer itself as the look-up table, checking screen co-ordinates for certain colours or text characters.)

Look up table techniques can also be used for 3D space but large areas would obviously not be practical and care would be needed to ensure that the storage requirements didn't go through the roof.

In 3D space, the 3D problem can be broken down into a set of 2D problems by applying certain restrictions. For example, all panels could be restricted to alignment with the primary planes and have edges aligned with the primary axes. This allows the collision detection process to become little more than a series of decision statements, checking each co-ordinate value in turn. Fine if simple box shaped areas are all you require.

The best way to detect collision in 3D space is to use a generic collision detection algorithm as this allows your game engine to cope with any type of panel and so allows maximum flexibility in the level design. The disadvantage is that generic algorithms are expensive if performed in real time.

This section describes the maths behind the generic collision detection algorithm used in Corridors of Power. Most collisions in the game use this algorithm and all collisions are calculated in real time. This is quite expensive but allows maximum flexibility in the future, e.g. I could have random scenery deformation and the game engine will cope with it quite happily. Also the hit will be less important in the future as CPUs gain power and more of the graphics pipeline is offloaded to the graphics card.

I can't take credit for the basic algorithm, it was developed by John Bradley. I took the algorithm, added the maths required to allow sliding, etc and coded it. The algorithm relies on a good basic knowledge of vector maths so dust off those old text books if you're a bit rusty.

The figure below shows the intercept of a vector, v, with a panel. P is the point of origin for the vector, e.g. a player's position. n is the panel normal and I is the intercept point.

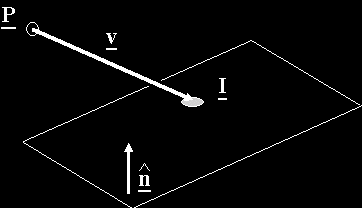
If the length of vector v is R we can state that:

The vector form of the equation of a plane is:

where Po is any point on a plane. Therefore for I to be on the plane:

substituting (1) for I in (3) and simplifying gives:

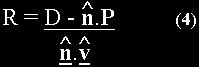
The panel determinant, D, can be calculated by using any of the panel's vertices in (2). If n.v is equal to zero then the panel is parallel to v and there can be no intercept. If n.v is greater than zero then the panel is not facing the viewer and may not need to be processed. If the range, R, is less than zero then the panel is behind the viewer and so again may not need to be processed further.

Using the range, R, in (1) allows the intercept point on the panel's plane to be determined. The final stage of the process is required to determine if the intercept point lies within the bounds of the panel as shown in the figure below:

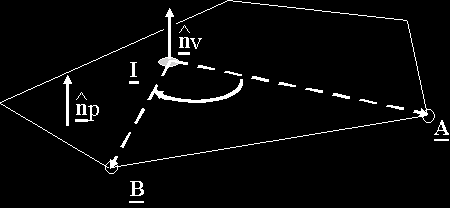
For the point I to be inside the panel, the angle between successive vectors from I to the successive panel vertices A, B, C, etc must be of the same sign. Taking the case that the panel vertices are defined in a clockwise sense from the viewing side, the cross product of the two vectors gives a normal:

If this normal is in the same direction as the panel's normal then:

The above process is repeated for each triangle formed between a pair of adjacent panel vertices and the intercept point. If the dot product is less than zero for any set then I is not contained within the panel and there is no collision.

NB: The above test only works if the vertices are specified in a clockwise order. If a counter-clockwise order is used then the order of the cross product in (5) or the sign of the comparison in (6) will need to be reversed.

I have found that the processing time for the routine can be reduced significantly by removing the square root calculation from (6). In this equation only the sign is of importance, so nv can be used directly in place of its unit vector.

To detect collisions with any panel you just plug the panel and viewer parameters into the algorithm and get a hit or miss answer. However, with some things it is not quite so straight-forward, the main exception being objects. Objects tend to contain a large number of small polygons and you normally don't need to test collisions with every single panel and this would be very expensive. The way around this is to define a panel or a set of panels that represent the outline of the object and perform the collision testing on these.

When you're performing collision detection for moving objects things get a little more complicated. Problems that occur are clipping movement to a distance in front of the panel that is greater then the near clip plane, sliding the object along the surface of the panel to preserve its momentum, coping with corners (particularly convex ones). I'll probably expand on this area later, but for now I'll leave all that up to you. All the problems are solvable using the same level of maths that I outlined in the previous section.